Neural Machine Translation by Jointly Learning To Align And Translate
Abstract & Introduction
-
Transformer, Bert 등 많은 기계 번역 모델이 Attention으로부터 출발했습니다.
1.1 소개
- Attention Mechanism은 “Neural machine translation by jointly learning to align and translate(2015)”이라는 논문에서 처음 제시되었습니다. Attention이라는 말이 직접 쓰이지는 않았지만 논문에서 다루는 내용을 보면 지금 우리가 부르는 Attention Mechanism의 골격을 볼 수 있습니다
- 이전까지 seq2seq가 기계번역에서 encoder-decoder구조를 사용해 $(i)$비약적인 성능향상과 $(ii)$길이가 가변적인 input에 대한 처리 라는 문제를 해결했지만 여전히 장기 의존적인 문제로 인하여 문장의 길이가 어느 수준 이상 넘어가면 정보를 온전히 끝까지 보전하기 어려웠습니다
- Attention Mechanism은 이런 문제를 해결하기 위해 마치 인간이 번역을 할 때 처럼 문장의 어느 부분에 “집중”할 수 있도록 학습시키는 방법을 말합니다
1.2 Contribution
- seq2seq 구조를 사용하되, encoder-decoder 구조에서 오던 병목현상을 새로운 알고리즘(Attention)으로 해결
- (후에) 많은 기계 번역 모델의 base가 되었음
1. Background : Neural Machine Translation
-
기계 번역은 sentence $\mathbf y$에 대하여 주어진 input $\mathbf x$을 이용해 $arg\ max_{\mathbf y}p(\mathbf y\mid \mathbf x)$ 를 구하는 과정
1.1 RNN encoder-decoder
- Encoder : input $\mathbf x = (x_1,x_2,…,x_{T_{x}})$를 fixed dim vector $c$로 바꾸는 encode과정. where $h_t = f(x_t,h_{t-1})$이고 $c = q(h_1,h_2,…,h_{T_{x}})$. $f$와 $g$는 비선형 함수
- Decoder : $p(\mathbf y) = \prod_{t=1}^Tp(y_t\mid {y_1,…,y_{t-1}},c)$ context vector $c$는 decoder의 첫 hidden state로 쓰이고 직렬적으로 decoder의 $t$시점의 output은 $t+1$ 시점의 input으로 들어가
token이 생성될 때 까지 반복된다
2. Learning To Align And Translate
-
여기부터는 논문의 서술과 다르게 Attention이라고 부르겠다. 논문은 Decoder부터 설명했는데 논리의 흐름을 보면 역순으로 설명하는 것이 이 알고리즘이 아예 처음 발표되었을 때 읽는 이로 하여금 이해가 쉽게하기 때문에 일부러 뒤집어 둔 것이란 생각이 든다. ($\mathbf y$는 이렇게 계산→파라미터는 어떻게? → 그건 어떻게?→…→input $\mathbf x$ 이런 논리다)
2.1 Encoder
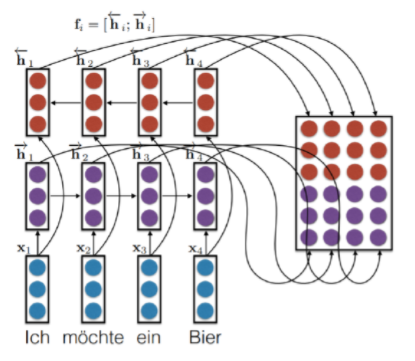
- 각 sentence sequence를 embedding한 input을 양방향 RNN에 넣은 값을 concat한다. 여기서 $i^{th}$열의 성분은 $i^{th}$번 째 입력 토큰의 양방향 RNN의 output임에 주의한다
2.2 Decoder
- 아래 그림은 [유튜브]에서 이미지를 발췌한 것인데 난해한 부분이 있다고 생각합니다. 대부분의 경우에 입력 seq의 길이와 출력 seq의 길이가 다를텐데 $x_T, c_T$를 $x_{T_x},c_T$로 적어 혼동을 없애야하지 않을까요..
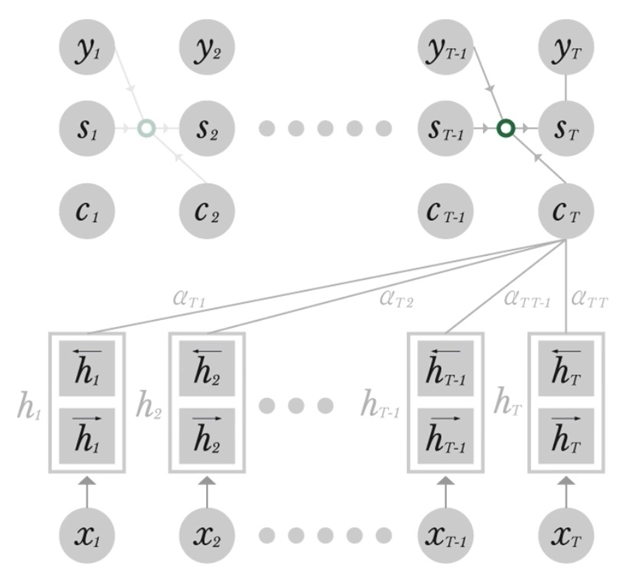
$$(1)\ e_{ij}=a(\mathbf s_{i-1},\mathbf h_j)\\(2)\ \alpha_{ij}=\frac{exp(e_{ij})}{\sum^T_{k=1}exp(e_{ik})}\\(3)\ \mathbf c_T=\sum^T_{j=1}\alpha_{Tj} \mathbf h_j\\(4)\ \mathbf s_t=f(\mathbf s_{T-1},\mathbf y_{T-1},\mathbf c_{T})$$
- $\alpha$는 scalar로 attention weight이다. 각 시점에서 $y_i$를 추정할 때 $h_T$에서 어느 부분(열:column)을 얼마나(weight) 반영할지 정해준다. 아랫 첨자 i와 j는 각각 <출력 $y$에서의 index>와 <양방향 hidden state $\mathbf h$에서의 column index>을 의미한다. $\alpha_{ij}$가 softmax 함수를 통해 구해졌다는 것으로 이것이 전체 대비 반영 비율(0~100%)을 표현하기 위해 쓰여진 식임을 알 수 있다
- $\alpha$와 $e$는 scalar임에 유의
여기부터는 헷갈리는 내용이 많으니 세세하게 차근차근 서술하겠습니다.
- 그렇다면 $\alpha$를 구하기위해 쓰인 $e$는 무엇일까? 우선 (1)식의 $a$는 선형 식이다. (caution !!! $\alpha \neq a)$
- (1)식의 $s_{i-1}$는 decoder에서의 hidden state이다. $h_j$가 무엇일까? encoder에서의 $\mathbf h$가 기억날 것이다. $h_j$는 $\mathbf h$의 $j^{th}$ column으로, $j^{th}$입력 token에 대한 정보가 담겨있다. 즉 $a(\cdot)$은 decoder의 hidden state와 특정 위치의 input에 대해 얼마나 유사도가 있는지 살피는 선형 함수다
- (어떻게 보면) $\alpha_{ij}$는 이것을 [0,1]사이에 있도록 조정해주는 역할이었을 뿐이다
- $\mathbf c_T$는 attention이 반영된 벡터로 T시점의 출력이 입력의 어느 부분에 집중하고 있는지 살필 수 있다. decoder의 context vector이다
3. Experiment Settings
- Encoder-Decoder 방식과 완전히 같은 데이터(WMT14)로 같은 Task. 같은 measure사용하여 비교하겠다
- encoder-decoder RNN vs research RNN에 대해 각각 up to 30, 50개 length의 sentence로 학습시킨 모델을 사용했다. 양쪽모델 encoder decoder모두 gate unit이 1000개 씩 있다
- train set에 변형을 가함. bag of words를 제한하여 일부 단어들을 모델에게 학습시키지 않음. test과정에서 이 제외된 단어들이 포함된 문장을 입력시킴으로서 성능평가하는 과정을 추가함
4. Results
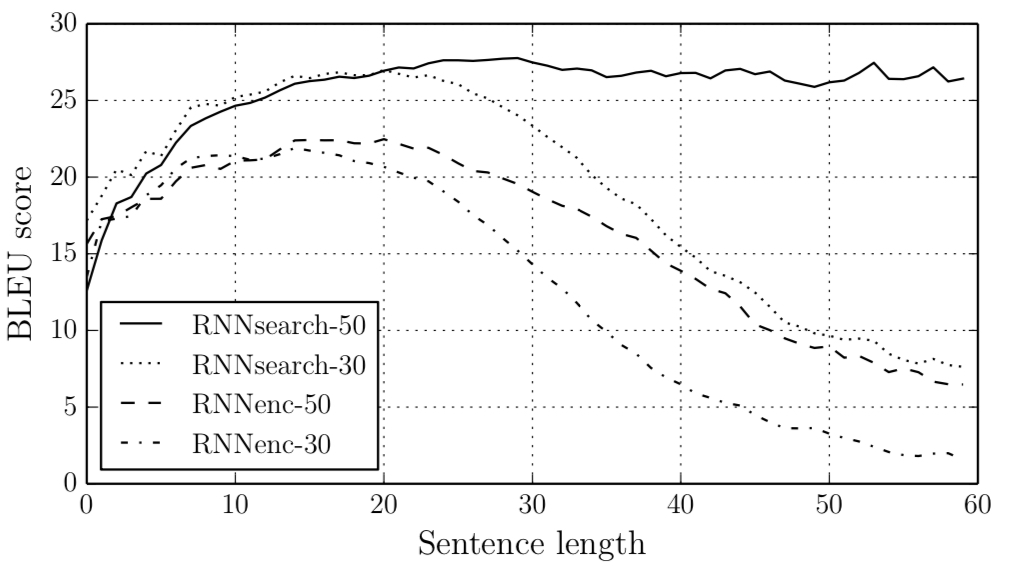
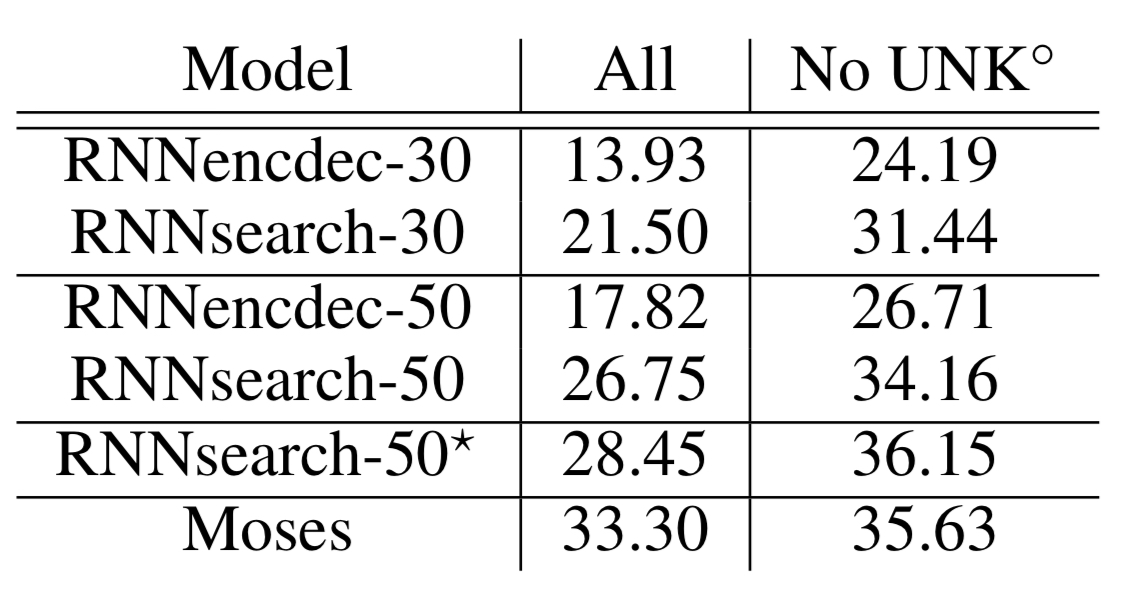

Reference
- 유명한 알고리즘이지만 그만큼이나 인터넷에 2% 잘못된 정보가 많다. 아래 첨자가 틀렸다던가 각 parameters의 해석이 난해하다던가…
- 아래 블로그는 정말 잘 해설해두셨다
https://ratsgo.github.io/from frequency to semantics/2017/10/06/attention/