Sequence to Sequence Learning with Neural Networks
Abstract
- DNNs가 여러 task에서 좋은 performance를 냈지만 seq to seq 문제에 DNNs구조는 mapping되지 못함
- 따라서 본 연구는 Deep LSTM구조를 활용해 input seq를 고정된 차원의 벡터로 encode하고 또 다른 Deep LSTM구조로 decode하고자 함
- Task는 번역이며 WMT-14 dataset (영어→불어)이 쓰였다
- 모델 measure는 BLEU score로 이루어짐
- 비교를 위해 통계적 언어모델인 SMT system과 성능비교가 이루어짐
- LSTM쪽 성능이 좋았다. 특이하게도 input데이터의 순서를 reverse한 데이터(target은 그대로)로 함께 학습했을 때 performance가 더 좋았다고 하는데 입력 source와 target 문장사이의 단기의존성을 더 높였기 때문이라고 저자는 서술했다
$$BLEU = min\left (1,\frac{output\ length(output)}{reference\ length(target)} \right )\left( \prod_{i=1}^{n}precision_{i} \right )^{\frac{1}{n}}$$
1. Introduction
- 지금까지의 DNNs는 input dimension이 고정되어 있어서 가변적인 input과 output의 길이를 가지는 번역, QA에서 한계를 가짐. 이것을 seq to seq problems 라고 하겠다
- Encoder & Decoder 구조를 제안한다. Encoder에서는 여러 길이의 input을 정해진 차원의 벡터로 임베딩하여 LSTM레이어(이 논문에서는 4개 층 사용)를 통과해 context vector를 생성한다. 이때 context vector 역시 고정된 길이의 벡터이다
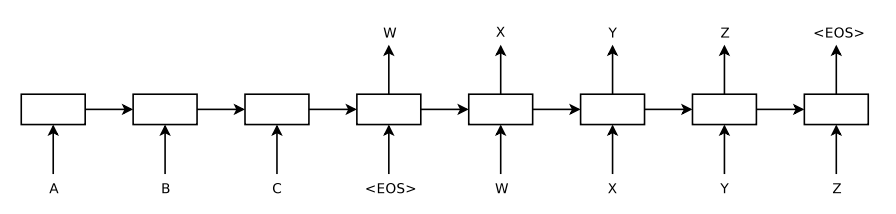
- 그렇다면 어떻게 다른 길이의 input과 output을 예측하는 것일까? <EOS : End Of Sentence> token을 받으면 인코딩이 끝나고 decoder를 통해서 output을 낸다. 이 출력값이 다시 input으로 들어가 다음 output을 예측
- 입력
토큰 input의 결과로 나오는 마지막 hidden state $h_{t}$가 context vector로 쓰인다 - 그림은 “ABC”순으로 그려져있는데 실제로는 “CBA” 순으로 넣었음에 주의한다
- 모든 입력 단어는 1000차원으로 임베딩된 벡터이다
2. The Model
$$h_{t} = \sigma (W^{hx}x+W^{hh}h_{t-1})\\
y_{t} = W^{yh}h_{t}$$
- 위의 전통적인 RNN 알고리즘은 input seq으로 $(x_{1},…x_{T})$ , output seq으로 $(y_{1},…,y_{T})$ 가 쓰일 때 사용되었다. 하지만 입력과 출력 seq길이가 다르면 사용할 수 없었다
- 따라서 encode - decode식의 방법이 제안되었다
$$p(y_{1},...,y_{T'}|x_{1},...,x_{T}) = \prod_{t=1}^{T'}p(y_{t}|v,y_{1},...,y_{t-1})$$
- $T\neq T’$임에 유의. LSTM을 활용한 seq2seq모델은 길이가 다른 input과 target에 대하여 인풋 sequence 길이 $T$에 대한 $T’$의 조건부 확률로 볼 수 있다. 이 때 encoder가 인풋 sequence를 하나의 vector로 바꾸기 때문에 input을 $v$로 표현할 수 있다
- 모든 $p(y_{t}\mid v,y_{1},…,y_{t-1})$는 vocabulary에 대한 softmax 확률로 출력된다
3. Experiments
- WMT’14에서 12M개의 subset을 train에 사용했으며 여기에는 348M의 불어 문장과 304M개의 영어 문장이 있다. bag-of-words는 가장 많이 쓰이는 단어로 뽑았으며 input언어가 16만개, target언어가 8만개로 고정되었다. out-of-vocabulary word는
token으로 대체되었다
$$(1)\ 1/|S| \sum_{(T,S)\in S}\log p(T|S)\\(2)\ \hat{T} = \arg \underset{T}{max}\ p(T|S)$$
- (1)은 Train에 관한 equation으로, source $S$ 로 target $T$ 를 출력하되 log probability를 최대화하도록 학습되었다
- (2)는 Train 후 예측에 관한 equation이며 $\hat {T}$를 예측 할 때 $S$에 대한 조건부 확률이 최대가 되게하는 $T$ 를 출력한다
- greedy search 방식이 아닌 beam search를 시도했다. 깊이를 다양하게 조정하여 수행했다
- input soruce를 reverse하여 넣으니 BLEU score가 25.9에서 30.6으로 상승하였으며 모델의 perplexity는 5.8에서 4.7로 감소했다
-
저자들은 이 현상의 원인에 대해서 완벽한 이유를 규명하지는 못했다.(While we do not have a complete explanation to this phenomenon, ~) 하지만 많은 short term dependencies의 영향으로 예상한다. 언어에서 유의미한 키워드는 앞에서 오는 경우가 많으므로 뒤집에서 해석하는 것이 성능이 좋았을 것이라 추측한다
Training Details
- 모든 LSTM의 파라미터를 (-0.08,0.08)로 uniform distribution 초기화
- SGD w/o momentum, lr=.7, 5epcoh이후 lr을 반으로 줄임. 총 7.5epoch(?) 학습
- LSTM에 기울기 폭발문제가 있다. 따라서 실험에서 gradient가 [10,25]에 있도록 treshold를 넘으면 스케일링을 진행. 스케일링은 모든 미니배치에 대해서 $s=\mid\mid g\mid\mid_{2}$를 계산함( 여기서 $g$는 gradient / 128 ). 만약 $s$ > 5 였다면 $g = \frac{5g}{s}$ 를 사용했다.
- 문장마다 길이가 다르다. (seq가 다르다) 대부분의 sentence는 20-30 단어로 구성되어있어서 128개의 minibatch로 랜덤하게 골라 사용했다. 하지만 일부 긴 sentence는 computation resource를 낭비한다. 긴 문장끼리는 따로 뽑아서 학습시켜 2배정도의 학습시간 향상을 보임
- 4개 층의 LSTM Layer가 사용됨
Training Results
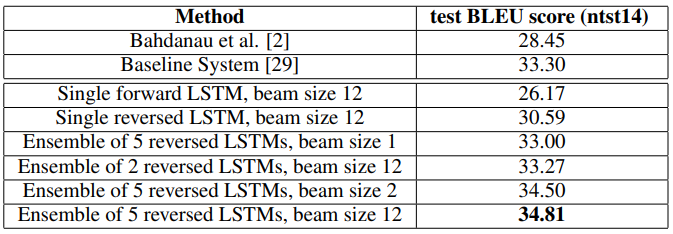
- bema size = 2에서도 size 12만큼이나 충분히 좋은 성능을 내었다
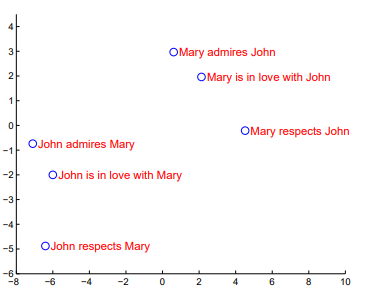

- PCA로 2차원에 plot한 모습. 비슷한(똑같은) 뜻을 가진 문장끼리 비슷한 위치에 임베딩된것을 확인할 수 있다
4. Conclusion
- seq to seq problem을 해결
- input sequence를 뒤집어 넣는 창의적인 방법
- Most importantly, 이제 처음 제시된 LSTM기반 (즉, 딥러닝 기반) 기계번역이 오랜기간 충분히 연구된 통계기반 모델의 성능을 앞지를 수 있음을 확인하였음