Set Function for Time Series

Abstract

• irregulary sampled time series를 위한 방법론과 모델을 제시함
• 이러한 데이터는 multi variable하고 특히 health care분야에서 많이 관찰 할 수 있음
• 관찰은 classification outcome을 도출함

1. Introduction

• 다양한 모델이 varying length of dataset에 적용될 수 있지만 이러한 모델들은 정규화된 샘플링이나 측정된 시간이 모든 mordality에 synchronized해야한다
• 또한 강제로 scale된 sequence 데이터는 정보의 손실이 생긴다
• SeFT(Set Function For Time Series) 구조는 $(i)$irregular한 sampling과 $(ii)$unsynchronized한 데이터에 적용될 수 있음

2. Proposed Method

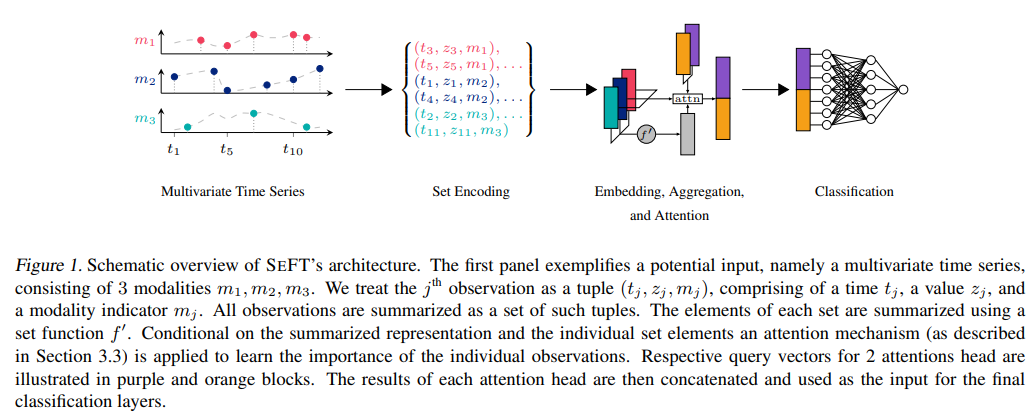
2.1 Notation & Requirements

Def 1 (Time Series)

• $\mathcal S_{i} =: ({s_{i},…s_{M}})$ 으로 정의. $s_{i}$는 tuple로 나타내며 $(t_j,z_j,m_j)$으로 각각의 성분을 표현할 수 있다. $m_{j}\in {1,2…,D}$으로 $D$는 time series의 dimension. $m$은 modality를 표현한다. 논문에서 예시로 바이탈 사인의 종류들이 여기에 해당됐다. $t$는 시점이고 $z$는 그 시점에서의 관측치
• 이 방법은 어떠한 정보도 손실하지 않으면서 불규칙하며 결측이 있고 synchronized하지 못하게 관측된 다변량 변수를 set에 저장할 수 있다

Def 2 (Dataset)

• $\mathcal D =: {(\mathcal S_{1},y_{1}),…,\mathcal (S_{N},y_{N})}$으로 표현 $y_i$는 Class 중 하나의 값을 가지고 $\mathcal S_i$는 $i^{th}$ time step을 나타내겠다
• 예를 들어서 $i$가 denotes 병원에 입원한 환자라고 하자. 환자 $i$의 vital sign으로 HR(심박수), MAP(혈압)이 측정되고 있고 HR은 0.5h 3h에 기록되었고 60,65의 관측치가 있다. 또한 MAP는 0.5h, 1.7h, 3h에 기록되었고 각각의 관측치가 있다면 $\mathcal S_i$를 아래와같이 표현할 수 있다

• 위의 예시에서 set은 modality가 증가하는 순서대로 저장되었다. 하지만 SeFT에서는 이 순서가 쓰이지 않음을 다시 상기한다. 하지만 이것이 시계열성을 버리겠다는(“throw away”) 의미가 아님에 유의한다. 정보는 손실되지 않고 tuple형태로 모두 가지고 있으며 encode와 aggregation 과정에서 한번에(“all at once”) 처리된다

Def 3 (Non-synchronized time series)

• $\mid {(t_k, z_k, m_k) \mid t_k = t_j}\mid \neq D$
• 그러니까 모든 관측치에 대해서 length가 같을 필요가 없더라. (실제 데이터 측정에서 모든 것을 완벽하게 동시에 측정하거나 통제할 수 있는 상황 X)

2.2 Model

• $h: \Omega\rightarrow \mathbb R^d$ 이고 $g :\mathbb R^d \rightarrow \mathbb R^C$ 겠다. 여기서 $d$는 Dim이고 $C$는 Class차원
• 위와같은 set function을 거치고 임베딩 후 class의 차원에 맞게 다시 임베딩해준다. 어떤 정보를 모델이 봐야할지 결정하기 위해 attention이 쓰인다. 후에 서술

Time Encoding

• positional encoding을 해준다. where $k \in {0,1,…,\tau/2}$
• 저자는 모든 $t_j$에 대해서 time encoding을 했다. 모든 $s_j$에 대해 $s_j = (x(t_j),z_j,m_j)$

2.3 Attention Based Aggregation

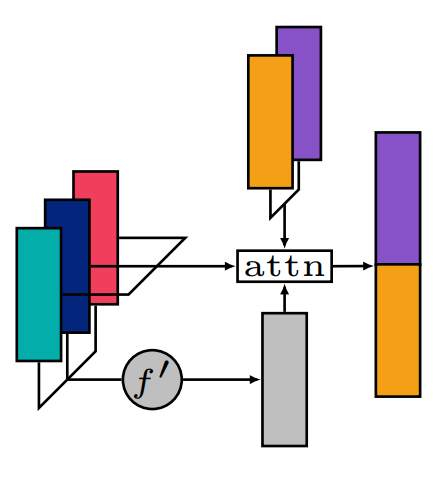
• 지금까지 임의 크기의 set을 fixed-size representation으로 encoding했다. 그러나 encoding된 set의 size가 들어나면서 irrelevant한 관측치가 더러 set function에 영향을 미친다.
• mean aggregation이 흔히 쓰이는 방법이지만 set size가 커짐에 따라 irrelevant한 값에 취약하다. 따라서 weighted mean을 추가로 제시한다. weighted mean은 마치 set input에 대해서 attention처럼 작동한다

2.4 Loss Function

• 달리 언급하지 않는 경우 $h$와 $g$를 multilayer 신경망으로 보겠다. $\theta$와 $\psi$는 각각의 parameter
• $l(\cdot)$ denotes NN $g_{\psi}$에서 sigmoid activation활용한 binary 분류의 cross-entropy loss

4. Experiments

• Appendix 3. 가면 접근이 까다로운 데이터에 access할 수 있는 코드와 baseline model 및 SeFT모델의 코드 링크가 있다. 이를 활용해 논문의 내용을 직접 실험해볼 수 있다

• [링크]

  4.1 Dataset

  • benchmark set 대신에 irregular하고 unsynchronized한 데이터 사용

    M3M

    • Hour 단위로 기록됨
    • Wide range of physiological measurements (e.g. MAP and HR)
    • M3M task의 목적은 처음 환자가 ICU에 입장하고 48시간 이내에 사망할지 예측
    • 21000개의 case가 존재하고 이 중 10%가 사망

    Physionet 2012 Mortality Prediction Challenge

    • 12000개 case의 적어도 48Hours 동안 ICU에서의 기록
    • 각 환자의 기초 정보는 ICU입장과 동시에 조사됨
    • 적어도 37개의 time seies data가 측정됨(혈압, 심박수 등)
    • 각 특성마다 일정한 시간간격으로 측정되었지만 어떤 것은 필요할 때만 측정
    • 목적은 역시 환자들의 생존여부를 예측하는 것

    Physionet 2019 Sepsis Early Prediction Challenge

    • 3개의 US 의료기관에서 60000 환자의 case
    • 40개의 variables가 있고 Hour단위로 값들이 기록됨
    • Task는 6-12H 이내에 폐혈증이 발생할지(onset) 여부

  4.2 Experiments Setup

  • 모든 모델이 똑같은 batch에 의해서 학습됨
  • 30 epochs
  • train에서 val 성능이 제일 좋은 것이 대표로 뽑힘

  4.3 Results

  

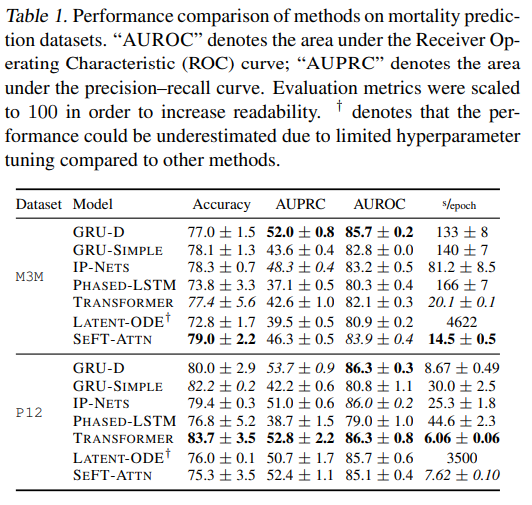
  Figure 4 . M3M데이터와 P2012데이터에 대해 여러가지 모델과 비교한 성능

  

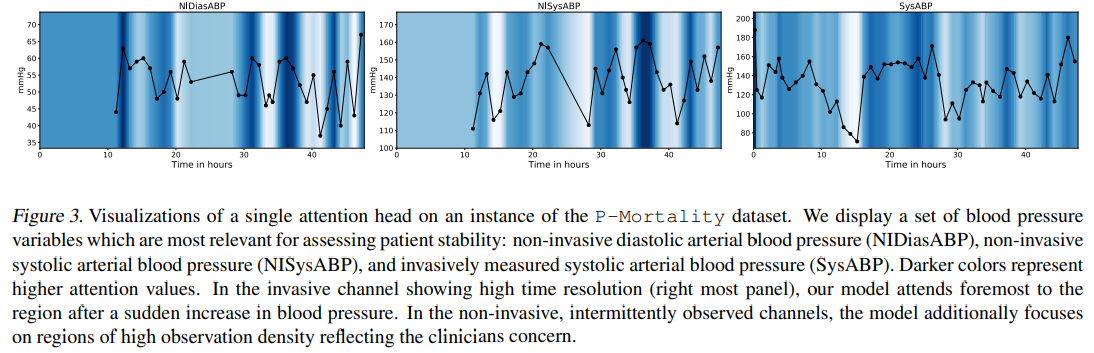
  Figure 3. Model이 어느 부분이 attention했는지 dataset의 변수별로 plot했다. 색이 진할 수록 attention