[Presentation : Paper seminar]Simple and Scalable Predictive Uncertainty Estimation Using Deep Ensembles
Abstract
- DNNs의 성과와 별개로 Uncertainty를 구하는 것은 또 다른 challenge. 현대 딥러닝 모델은 overconfident한 문제를 가지고있다
- 지금까지는 Bayesian-NN을 활용해 uncertainty를 구했지만 많은 파라미터 수정과 계산을 요구했다.
- 따라서 본 연구에서 병렬적으로 uncertainty estimation이 가능한 Non-Bayesian 방법을 제시한다
1. Introduction
- DNNs의 overconfident 문제는 practical application에 어려움을 준다
- 연구에서 두 가지 평가 measure에 중점을 두었는데 첫째로 calibration성능이다. 모델은 정확할 수 있으나 miscalibrated할 수 있기 때문이다. 둘째로 domain-shift에 대한 robustness이다. 강건성이 보장된 모델은 실용적 활용 가치가 높다
- 지금까지 MCMC, 라플라스 근사 등 uncertainty를 측정하고자한 시도가 있었다. 가장 근본적인 해결책은 베이지안 방법론이지만 많은 연산을 필요로 하기에 DNNs에서 사용하기 힘들었다
-
최근 Monte Carlo dropout(MC-dropout) 방법론이 주목할만한 performance를 보였다. dropout은 마치 ensemble of NNs로 생각할 수 있다. 또한 앙상블은 training data의 분포로 사후확률은 근사하는 베이지안보다 덜 training data의 분포에 의존적이다. 이런 아이디어에 기반해 새로운 방법론을 제시한다
Contributions
- First, simple하면서도 scalable한 uncertainty estimation 방법론을 제시한다. 또한 $(i)$ ensemble $(ii)$ adversarial training 을 활용해 학습을 진행해보겠다
- Second, calibration과 일반화의 관점에서 uncertainty estimation의 quality를 측정하는 방법을 제시한다
2. Deep Ensembles
2.1 Problem setup and High-level summary
$$\mathcal D=\{\mathbf x_n,y_n\}^{N}_{n=1}\ ,where \mathbf x \in \mathbb R^D\\ y \in \{1,...,K\}\\ \{\theta_m\}^M_{m=1}\ ,where \ M \ denotes\ the\ Number\ of\ NN\_ensembles $$
- 논문에서 제시하는 recipe는 간단합니다. (1) proper scoring rule사용 as training criterion (2) AT(Adversarial Training) (3) train an ensemble
2.2 Proper scoring rules
- scoring rules는 predictive uncertainty의 quality를 measure한다. 수식 $S(p_{\theta},(y,\mathbf x))$는 predictive distribution $p_{\theta}(y\mid \mathbf x)$를 실제 $(y,\mathbf x)$의 분포에 대해 evaluation한다
- 많은 NN loss func에서 log-likelihood가 좋은 평가지표로 쓰인다. 특히 K개 class 분류의 경우 Brier score라는 측도를 쓸 수 있다. one-hot label된 true target $\delta$에 대해 확률분포의 확률값을 직접 빼서 square한 뒤 class의 개수만큼 평균을 내준 score이다
$$=Brier\ score=\\ \mathcal L(\theta)=- S(p_{\theta},(y,\mathbf x)) = K^{-1}\sum^{K}_{k=1}(\delta_{k=y}-p_{\theta}(y,\mathbf x))^2$$
2.2.1 Training criterion for regression
- 회귀문제에서 NN은 어떤 확률 분포가 아닌 single value $\mu(\mathbf x)$를 출력할 것이다. 또한 MSE에 기반한 loss를 계산한다. 하지만 MSE는 uncertainty prediction에 사용할 수 없다. 따라서 본 연구에서는 final network에서 두 가지 값을 출력하도록 설계했다. 첫째로 predicted mean $\mu(\mathbf x)$이고 둘째로 variance $\sigma^2(\mathbf x)>0$이다. 여러번 출력되는 단일 관측치들을 이분산성의 가우시안 분포로 가정하고 mean과 variance를 얻는다. NLL criterion을 최소화하는 방향으로 학습했다
$$-log\ p_{\theta}(y_n|\mathbf x_n)=\frac{log\ \sigma^2_{\theta}(\mathbf x)}{2}+\frac{(y-\mu_{\theta}(\mathbf x))^2}{\sigma^2_{\theta}(\mathbf x)} + constant$$
2.3 Adversarial Training to smooth predictive distributions
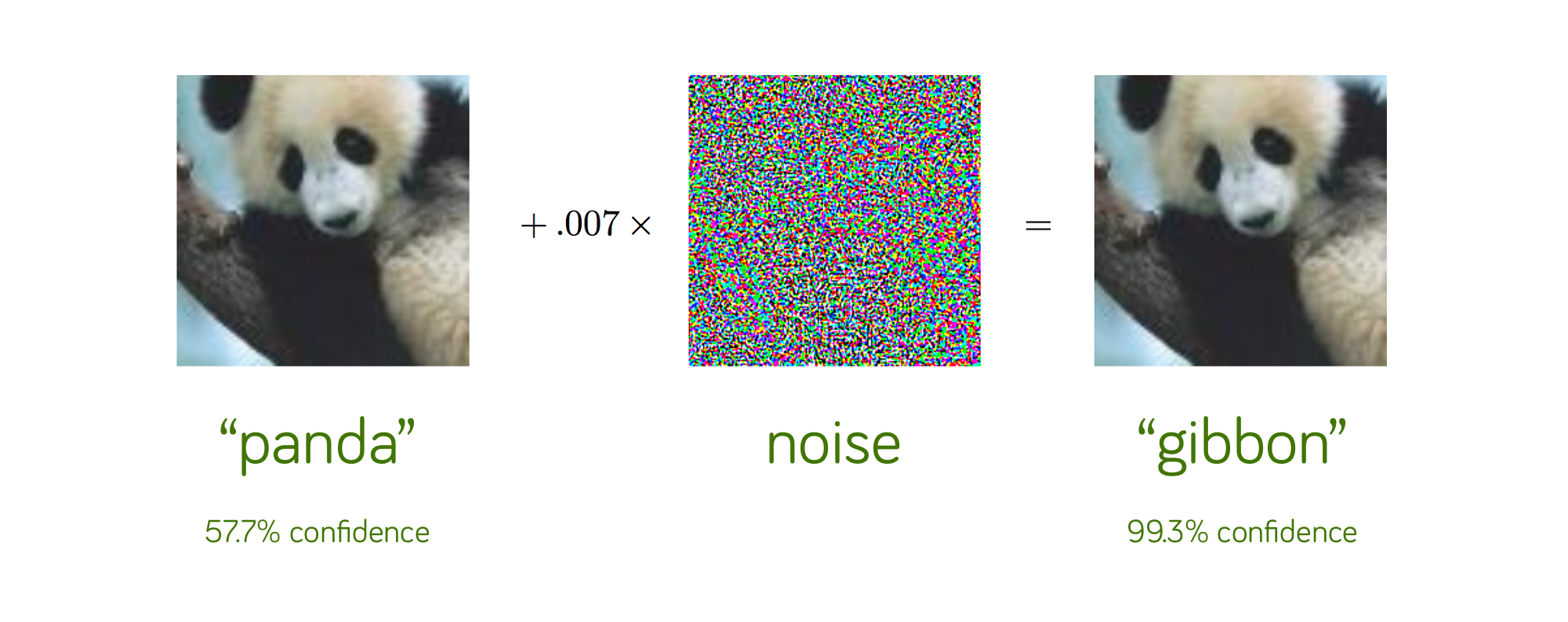
- classifier 부근에 위치한 data point들에 대하여 아주 작은 perturbation을 주어 loss가 커지는 방향으로 데이터를 변조시켜 모델의 예측 결과를 바꾸는 것을 adversarial attack이라고 한다. 오분류 자체의 문제도 있지만 이미지의 경우 사람은 전혀 알아채지 못하는 수준의 noise만으로도 DNNs을 오작동 시킬 수 있다는 점에서 보안의 문제도 있다
- 이런 adversarial attack(AT)에 robust(noise에 강건성을 가짐)하게 model을 학습하는 방법을 adversarial training이라고 부른다
- 저자는 AT이 예측분포를 더 smooth하게 해주어 더욱 robust한 결과를 낼 수 있음을 실험적으로 확인했다고 한다
$$FGSM \ :\ \widetilde{x} = x + \epsilon(\nabla_x \textit{l}(\theta, x,y))$$
2.4 Ensembles
- 실험에서는 bagging 방식이 쓰였다. Bootstrap이 약 63%만의 data sample를 활용하지만 DNN는 학습데이터가 많아지면 성능이 향상되는 특징이 있기때문에 모든 sample을 활용하여 학습했다. 연산의 병렬화를 위해서 sampling을 제외한 부분은 bagging방식 사용
왜 Bootstrap 방식의 sampling이 전체 데이터의 63%정도를 반영한다고 서술하였나?
$$\lim_{N\rightarrow \inf}(1-(1-1/N)^N) = 1-e^{-1} \approx0.632$$
N개의 sample이 있다면 1개의 sample을 뽑을 때 특정 sample이 뽑힐 확률은 1/N일 것이다. 단 한번이라도 뽑히지 않을 확률을 구하려는 것이므로 여집합의 확률을 구하면 된다. 한번이라도 뽑힐 사건을 N회 반복해 빼야하므로 N승 해준 뒤, 보통 ML에서 데이터셋이 충분히 크므로 극한으로 보내면 exponential의 정의에 의해 상기 값을 유도할 수 있다.
- 알고리즘은 아래와 같다. 앙상블 모델의 size는 $M=5$로 설정되었고 AT를 위한 섭동이 input $\mathbf x$의 $\mathbf D$의 1%로 설정되었음에 유의한다

- 위 논리대로 $M$개의 모델을 학습하고, $p(y\mid \mathbf x)=M^{-1}\sum^M_{m=1}p_{\theta_{m}}(y\mid \mathbf x,\theta_m)$ for 분류. 회귀문제의 경우 여러 모델의 mean과 variance를 mix해줘야 할 것이다. 이것은 mixture Gaussian 분포의 mean과 variance를 구하는 것과 같으며 그 식은 아래와 같다
$$M^{-1}\sum \mathcal N(\mu_{\theta_{m}}(\mathbf x),\sigma^2_{\theta_m}(\mathbf x))\\ \mu_{*}(x) = M^{-1}\sum_{m}\mu_{\theta_{m}}(x) \\\sigma_{*}^{2} = M^{-1}\sum_{m}(\sigma^{2}_{\theta_{m}}(x) + \mu^{2}_{\theta_{m}}(x))-\mu^{2}_{*}(x)$$
3. Experimental results
3.1 Evaluation metrics and experimental set
- 분류문제는 Negative Log Likelihood(NLL)과 앞서 살펴본 Brier score를 predictive uncertainty 평가에 사용했으며 회귀문제는 RMSE를 사용했다
- batch_size=100, Adam with lr=.1, fixed $\epsilon$ =0.01 for AT
3.2 Regression on toy datasets

- $y=x^3+\epsilon$ $,where\ \epsilon \sim \mathcal N(0,3^2)$에서 training examples를 뽑음
- 최우측, 앙상블을 사용했을 때 관측 데이터로부터 멀리 떨어져도 ground-truth가 회색 추정영역 안에 위치한 것을 확인할 수 있다
3.3 Regression on real world datasets
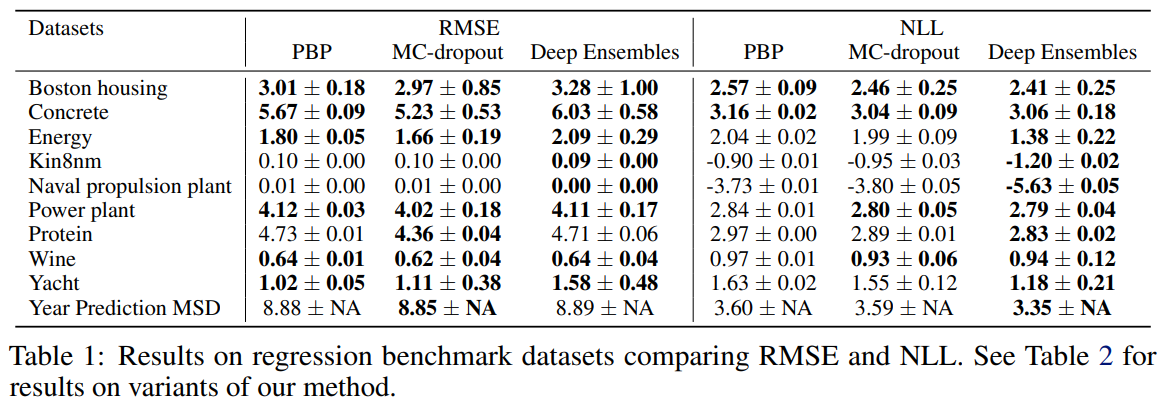
- RMSE의 몇몇 taks를 제외하고는 Deep Ensembles이 좋은 performance를 보여주었다
3.4 Classification on MNIST, SVHN and ImageNet
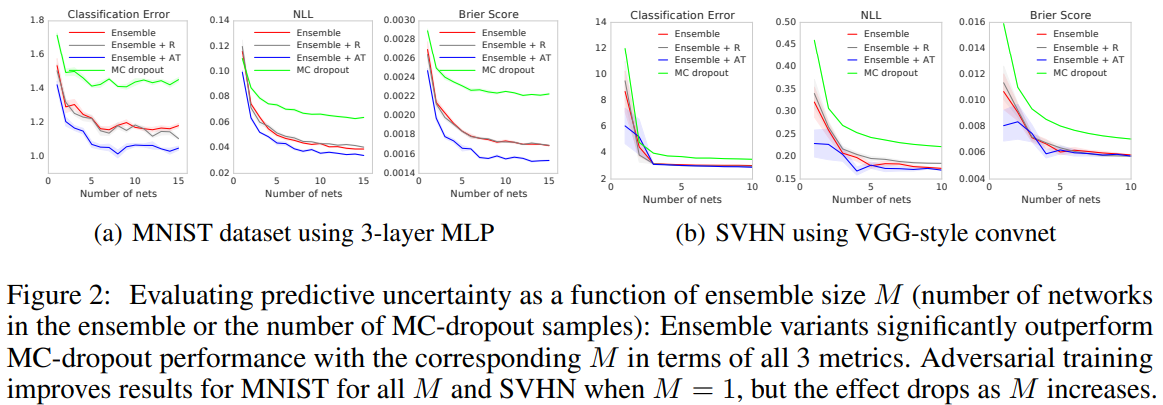
- AT와의 성능을 비교하기 위해서 random augmentation한 case도 학습했다. AT가 더 좋은 성능을 냈으나 augmentation에서도 역시 성능 향상이 보였다
- MNIST의 경우 $M$이 증가함에 따라 전체적인 성능 향상을 보였으나 SVHN에서는 $M=1$ 이후에는 그 효과가 미미했다. 만약 classes가 잘 calibrate 됐다면 AT이 classification boundary를 크게 바꾸지 않았을 것이다. 따라서 $M=1$ 이후의 미미한 성능은 추가적인 연구를 필요로한다
- ImageNet은 computing power 문제로 ensemble만 확인했으며 $M$이 증가할수록 세 가지 measure에서 좋은 성능을 보였다
3.5 Uncertainty evaluation: test examples from known vs unknown classes
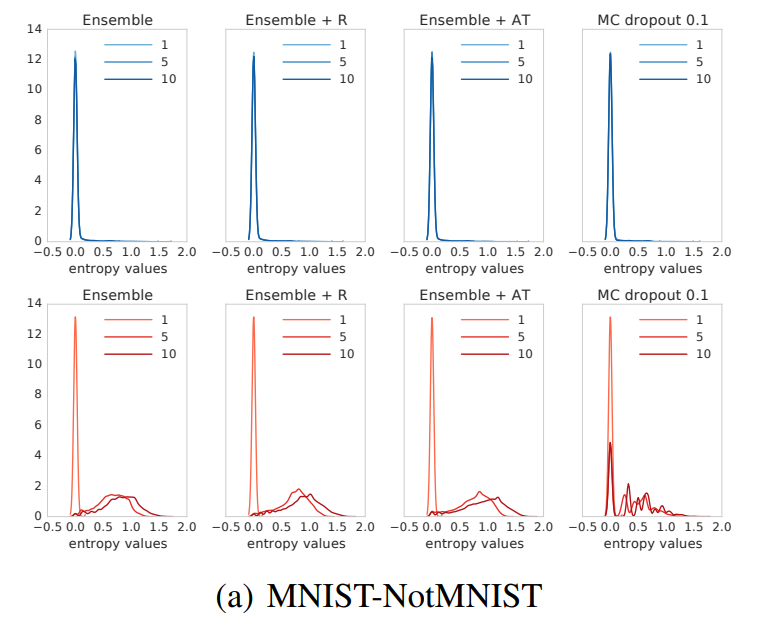
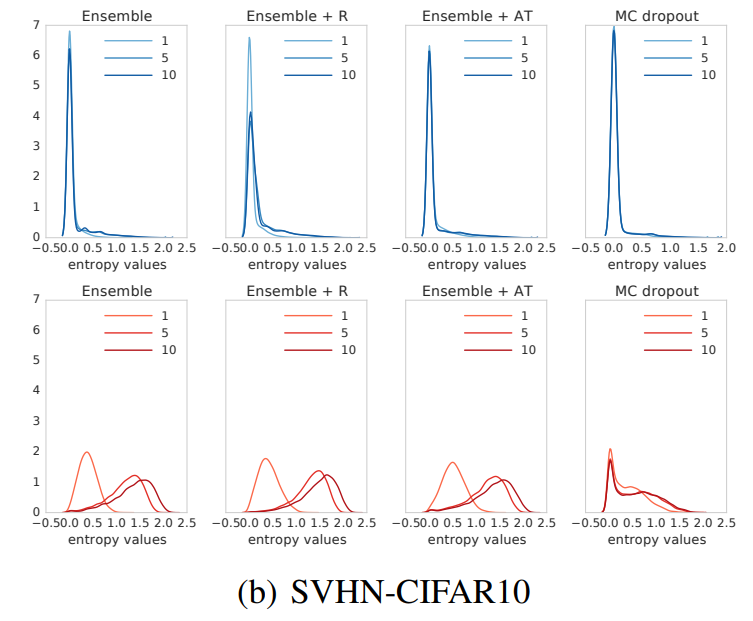
- unseen classes가 포있는 OOD example에 대하여 uncertainty를 평가한다. MNIST dataset으로 학습한 모델을 NotMNIST dataset으로 test한다. NotMNIST는 알파벳이 target으로 있는 분류 문제이다
- known classes(파란계열 그래프)에서는 앙상블이나 MC-dropout 모두 작은 entropy를 보였다. 하지만 unknown dataset에 대해서는 앙상블이 무질서도가 더 빠르게 증가했다. 이는 OOD에 대해서 앙상블 방법이 더 불확실성을 잘 표현한다고 할 수 있다
- SVHN-CIFAR10의 경우에도 MC-dropout은 판단할 수 없는 데이터에 대해 overconfident한 경향을 보였다
3.6 Accuracy as a function of confidence
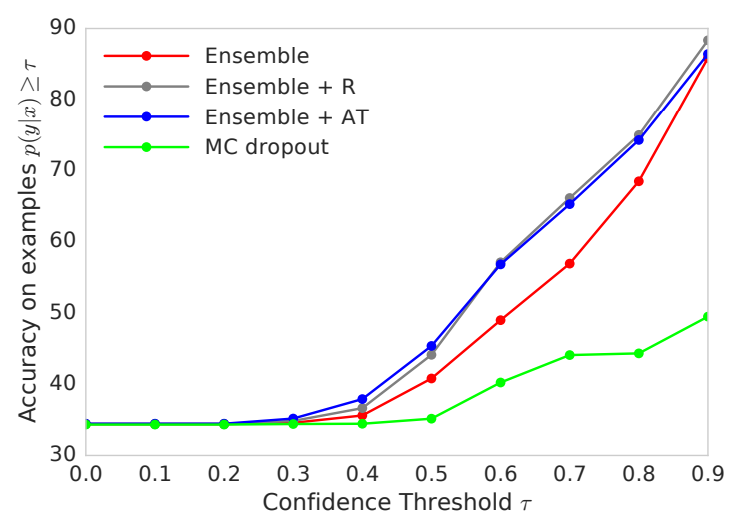
$$\hat{y} = arg\ max_kp(y=k|\mathbf x)\\confidence:\ p(y=\hat{y}|\mathbf x)=max_kp(y=k|\mathbf x)$$
- MNIST로 학습되었고 MNIST+NotMNIST mixture로 test되었다. MC-dropout같은 경우는 confidence가 높아도 accuracy는 높지 못하다. 즉 overconfident하다